How to Value Stocks & Buy at the Right Price
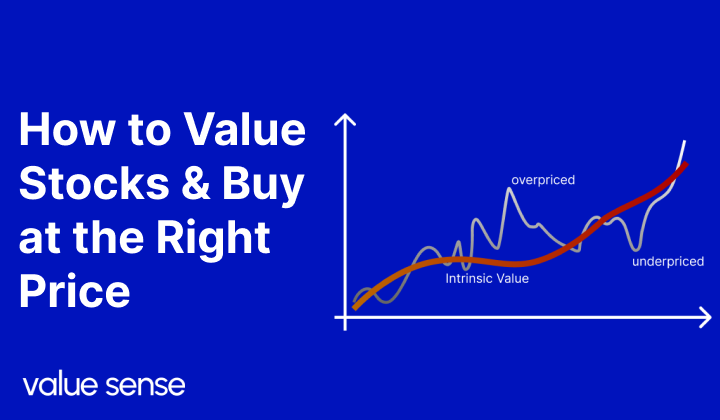
Value investing is simply buying businesses for less than what they are worth. By far one of the most proven ways of generating strong returns in the stock market.
Some of the most successful investors and now billionaires have adopted this approach - Warren Buffett, Peter Lynch, Joel Greenblatt, Seth Klarman, the list goes on.
In order to do this, you must be able to come up with a value for said businesses. While there are complex valuation techniques such as the Discounted Cash Flow Model, let’s look at a simple way to value a business.
LET'S LOOK AT A SIMPLE SMALL BUSINESS
We have an owner, Kevin. Kevin opens a soda business. He hires one person to run the business. Kevin isn’t going to do anything to help run the business.
Kevin’s soda business generates:
- $100,000 = Revenue
Costs are, $20,000 on wages, $40,000 on soda and $10,000 on rent:
- $70,000 = Total Costs
Income is:
- $30,000 = Income ($100,000 revenue – $70,000 costs)
Tax paid on the income:
- $10,000 = Taxation
Earnings are:
- $20,000 = Earnings ($30,000 income – $10,000 taxes)
SO, HOW MUCH WOULD YOU PAY FOR THIS BUSINESS?
Would you pay $400,000 for this business? How about $200,000? Maybe $100,000?
Let’s assume the business makes $20,000 per year, for the remainder of its lifetime. Let’s also assume the business has very little risk of failure.
If you paid $400,000 for this business, it would take 20 years for you to get your money back. (400,000 / 20,000 = 20 years)
That would be a return of 5% per year. (20,000 / 400,000 = 5%)
If you paid $200,000 for this business, it would take 10 years for you to get your money back. (200,000 / 20,000 = 10 years)
That would be a return of 10% per year. (20,000 / 200,000 = 10%)
If you paid $100,000 for this business, it would take 5 years for you to get your money back. (100,000 / 20,000 = 5 years)
That would be a return of 20% per year. (20,000 / 100,000 = 20%)
So the real question is, for the level of risk you are taking, what (reasonable) rate of return do you want to earn on your capital?
Working backwards from here is a good place to start.
Let’s assume you want a 10% return per year. That means you would not be willing to pay more than $200,000 for Kevin’s soda business.
HOW TO APPLY THIS TO STOCKS?
A stock simply represents a large company.
The owners include anyone that owns a share in the company (shareholders). There can be thousands of shareholders of a stock. The shareholders are represented by a group of people called the board of directors. The CEO and all the employees work for the owners (shareholders).
When looking at a stocks profits are often described as earnings and commonly written as Earnings per Share (EPS)
EPS is simply the net income divided by the total number of shares outstanding.
That is the earnings you would be entitled to if you owned a single share.A quick way to judge the price of a company is using the Price to Earnings Ratio (P/E Ratio). To calculate the P/E Ratio we simply divide the price of the stock by its EPS.
For example, if a stock had a price of $400 per share and an EPS of $20 per share, its P/E Ratio would be 20. (400 / 20 = 20).
We can then calculate the expected return we would get from this stock using Earnings Yield. To calculate earnings yield we simply divide 1 by the P/E Ratio. In the above example the Earnings Yield would be 5%. (1 / 20 = 0.5 = 5%).
If you only wanted to invest in companies that would generate you a 10% return, you would be looking at companies with a P/E Ratio of 10 or lower. (10 /10 = 0.1 = 10%)
SUMMARY
In the real world, earnings do not remain constant for the lifetime of a business. They increase and decrease over time. In order to accurately value a business, you must be able to somewhat forecast future earnings.
While the example above is an overly simplistic way to value a business, the key principles are there. Valuing a business is all about working out how much you are willing to pay for the business’s earnings.